极限是微分和积分的基石.函数在一点处的导数或微分本质上就是某个函数在一点处的极限,而函数在闭区间上的积分则是某个和式的极限.连续是函数可能具有的一个重要初等性质,也是通过函数的极限来定义的。本章将介绍数列极限、函数极限和函数的连续性.数列极限是函数极限的特殊情形,将为函数极限的深入学习奠定基础.函数的连续性可看做是函数极限的一个重要应用,也为函数微分的学习做好铺垫。
数列可看作自然数集上的函数,是一类特殊的函数.与实数集上的函数相比, 数列更简单、更直观. 接受并理解数列极限的定义有助于我们深入认识实数集上的函数在无穷远处或在一点处的极限,而实数集上的函数在一点处的极限是本课程的基石.另一方面,数列极限的定义是级数理论的基础.
数列极限在日常生活中有重要的应用.例如,在银行存款业务中,用复利计息就与数列极限有着密切的联系.
复利计息就是利息以一定周期不断转化为本金的过程,俗称利滚利.假设某客户在银行存了1万元(本金),年复利率为,我们考虑其一年后的本利和.
若计息周期为一年,则一年后本利和为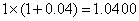 万元;
万元;
若计息周期为六个月,则一年后本利和为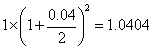 万元;
万元;
若计息周期为一个月,则一年后本利和为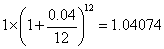 万元.
万元.
若计息周期为一天呢? 为一小时呢?
一般地,若计息周期为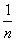 年,则一年后的本利和为
年,则一年后的本利和为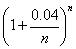 元.这样, 就得到无穷数列
元.这样, 就得到无穷数列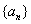 ,其中
,其中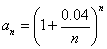 .对于不同的n,
.对于不同的n,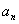 ,的取值见下表:
,的取值见下表:
| n | 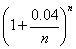 |
|---|---|
| 1 | 1.0400 |
| 50 | 1.0407941 |
| 100 | 1.0408024 |
| 150 | 1.0408052 |
| 200 | 1.0408066 |
| 250 | 1.0408074 |
| 300 | 1.040808 |
由上述列表我们猜测,数列可能是单调递增的,且当无限增大时,无限接近于某一确定的数值,这一确定的数大约为.事实上,这一确定的数确实存在,但不是,更多细节见后面章节.这一确定的数就是数列的极限.下面,我们给出数列极限的直观描述.
对于数列和给定的数,若当无限增大时无限趋近于,则称为数列的极限,也称数列收敛于.
在数列极限的直观描述中,“无限增大时”和“无限趋近于”是什么含义呢? 这样的文字描述无法用于严谨的数学证明或逻辑推理,不利于相关理论的发展.那么,数列极限的严格数学定义是什么呢?
对于数列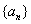 和给定的数a,若当n无限增大时
和给定的数a,若当n无限增大时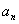 无限趋近于,则称a为数列
无限趋近于,则称a为数列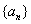 的极限.在该直观定义中,“n无限增大时”和“
的极限.在该直观定义中,“n无限增大时”和“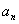 无限趋近于a”是主观的、感性的认识,如何用严谨的数学语言刻画呢?
无限趋近于a”是主观的、感性的认识,如何用严谨的数学语言刻画呢?
在数学中,我们通常用两数差的绝对值衡量两数的接近程度.如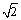 比
比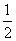 更接近于1,这是因为
更接近于1,这是因为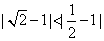 .从而,我们可以用
.从而,我们可以用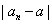 的大小衡量
的大小衡量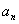 与a的接近程度.
与a的接近程度.
Copyright © 2024 河南理工大学.粤ICP备11037858号